Here Is The Math Problem:

Go ahead and try to solve this math problem. However, if you find that you are stuck, please continue reading as we show how to solve this problem 4 different ways! The four methods are: Relative Info, Logic, Common Sense, and Algebra.
RELATIVE INFORMATION APPROACH
1. Relative Information: To get a better understanding of this approach, let’s quickly solve a very simple distance problem:

To solve this problem, we need to divide the relative distance by the relative speed. The reason being, every hour, car 1 covers an additional (100 – 50) 50 km. Furthermore, if car 1 is behind by 150 km, then it would take 150km/50km/h = 3h to catch up to car 2. More importantly, now that this logic is cleared, let’s focus on solving the original problem:

The formula may seem confusing, but the R constant is the special value that allows us to find the actual distance while just knowing the relative distance. Note: The relative distance value in this problem isn’t as intuitive as it should be. Thus, let’s examine what it is and how it relates to our math problem:
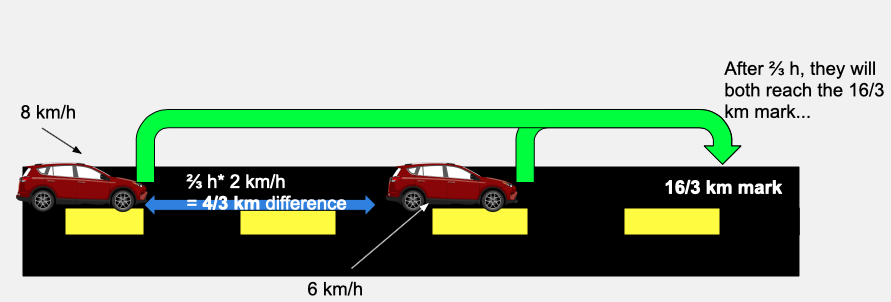
Furthermore, we can simplify our formula for distance to:

LOGICAL APPROACH
2. Now, let’s try the second approach to solving the problem: Logic. The biggest takeaway when looking at distance problems is that speed and time are inversely proportionate. Meaning, when the speed of the car goes up, the time taken to travel goes down. Likewise, when the speed of the car goes down, the time taken to travel goes up. Using this logic, we can come across another approach for solving this problem.

Thus, if travelling at 8 km/h results in ¼ (1 – ¾) of time saved (compared to when travelling at 6 km/h), then the difference in times is equal to 1/4 of the time taken while travelling at 6 km/h. Alas, if 1/4 is equal to 2/3 h, then 4/4 or 1 is equal to 8/3 h. Meaning, the distance between Adam’s home and office is the distance that takes 8/3 hours while going at 6 km/h. Moreover, since distance is equal to speed * time, we know that the distance is 8/3 * 6 = 48/3 or 8*2 = 16 km. Thus, the distance was 16 km.
COMMON SENSE APPROACH
3. Moving on, let’s try solving the problem using common sense: Let’s assume that the distance between the home and office is the lcm of 6 and 8, which is 24 km. Now, to travel 24 km at 6km/h and 8km/h, it would take 4h and 3h respectively. Hence, the difference in time would be 1h.
However, since the difference in time was 40 minutes (25 minutes early + 15 minutes late = 40 minutes difference in time), we need 2/3 of the difference in time. If we need 2/3 of the time difference, then we would also need 2/3 of the actual distance (as the time depends directly on the distance –> because the speed is not going to change). Now, let’s calculate 2/3 of 24 km… It is 16 km. Overall, using this lcm and ratio approach, we were able to common sensically solve the problem.
ALGEBRA APPROACH
4. Finally, let’s go through the old-school algebra approach. Although this may take the most time, it is sure to get you the right answer! Without further ado, let’s dive into it:

In conclusion, there are many ways to solve a problem. More importantly though, it is crucial to understand why a certain approach or solution works. In this example, we were able to arrive at 16 km distance using several methods. In conclusion, take some time to explore questions and try to find new and interesting solutions to the problem.
Not to mention, if you want to challenge yourself with another problem, check out our post on square numbers: 1452 * WHAT SMALLEST VALUE WILL GIVE YOU A SQUARE NUMBER?
Also, if you would like to find online helpers to solve equations (with steps), check out cymath. They provide solutions for numerous problems and can surely help you when you are stuck or simply want to confirm your answer.
Finally, if you enjoyed solving this math problem, then please both share with your friends and leave a nice rating! Thank you! 😀